Materi Integral SMK

Pengertian Integral

Integral adalah bentuk penjumlahan berkesinambungan (kontinu) yang merupakan anti turunan atau kebalikan dari turunan. Adapun contoh bentuk turunan adalah sebagai berikut.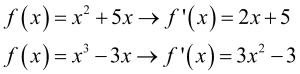

Rumus Dasar Integral

Adapun rumus dasar yang digunakan adalah sebagai berikut.
1. 
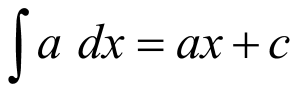
2.  
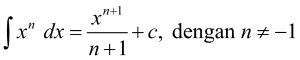
3. 

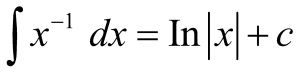
Jenis-jenis Integral

Berdasarkan bentuk hasilnya, integral dibagi menjadi dua, yaitu integral tak tentu dan integral tentu.

1. Integral tak tentu

Integral tak tentu adalah bentuk integral yang hasilnya berupa fungsi dalam variabel tertentu dan masih memuat konstanta integrasi. 

Oleh karena itu, rumus umum integral dinyatakan sebagai berikut.
, dengan c adalah konstanta integrasi

2. Integral tentu

Pada bahasan sebelumnya, telah dijelaskan tentang integral tak tentu di mana hasil dari integrasinya masih berupa fungsi. Jika hasil integrasinya berupa nilai tertentu, integralnya disebut integral tentu. Adapun bentuk umum integral tentu adalah sebagai berikut. 

dengan: x = a disebut batas bawah
x = b disebut batas atas
Arti dari bentuk integral di atas adalah suatu f’(x) diintegralkan atau dijumlahkan secara kontinu mulai dari titik a sampai titik b, sehingga hasil akhir yang diperoleh akan berupa angka, tidak lagi fungsi.

a. Sifat-sifat Integral Tentu

Apabila f(x), g(x) terdefinisi pada selang a, b, maka diperoleh persamaan berikut.
1. 
2. 
3. 
4. 
5. 

b. Aplikasi Integral Tentu

Seperti Quipperian ketahui bahwa integral bisa diaplikasikan dalam kehidupan sehari-hari. Salah satu contoh yang umum dikenal adalah luas daerah. Luas daerah yang dimaksud adalah luas daerah di bawah kurva. Adapun langkah menghitungnya adalah sebagai berikut.

• Batas daerah yang akan diintegralkan harus jelas. Adapun batas daerah yang dimaksud adalah batas kiri dan kanannya serta batas atas dan bawahnya. Bentuk batas daerah bisa berupa fungsi atau konstanta, fungsi linier dan nonlinier (kuadrat, pangkat 3, akar pangkat). Bagaimana jika salah satu batas belum diketahui? Quipperian harus mencarinya terlebih dahulu, agar luasnya bisa dihitung.
• Quipperian harus mampu menggambar daerah di dalam kurva sesuai dengan batas-batas yang telah ditentukan (jika gambar masih dinyatakan dalam batas-batasnya saja). Oleh karena itu, diperlukan kemampuan untuk menggambar dengan baik.
• Quipperian juga harus bisa menempatkan rumus yang tepat untuk menghitung luas daerah berdasarkan ketentuan yang telah ada. Jangan lupa untuk memperhatikan gambar daerah dan rumus yang bersesuaian. Quipperian jangan khawatir ya, setiap daerah memiliki rumus fungsinya masing-masing, contohnya berikut ini.

a) Bentuk daerah jenis 1

b) Bentuk daerah jenis 2

c) Rumus cepat mencari luas
Rumus cepat tidak berlaku untuk seluruh daerah ya, Quipperian. Rumus ini berlaku pada daerah-daerah yang memiliki kondisi berikut.

• Memiliki dua batas fungsi, yaitu fungsi kuadrat dan fungsi kuadrat.
• Memiliki dua batas fungsi, yaitu fungsi kuadrat dan fungsi linear.

Jika memenuhi dua kondisi di atas, luasnya dapat dicari menggunakan persamaan berikut.
Lalu, apa yang dimaksud dengan a, b, dan c? Ketiga konstanta tersebut diperoleh dari proses berikut.

• Jika fungsinya y = f(x) dan y = g(x), maka buat fungsi selisihnya y = f(x) – g(x).

Jika fungsinya y = f(y) dan y = g(y), maka buat fungsi selisihnya y = f(y) – g(y)

• Fungsi selisih yang sudah Quipperian dapatkan, jangan disederhanakan lagi agar teridentifikasi nilai a, b, dan c.
• Jika Quipperian sudah mendapatkan nilai a, b¸ dan c, substitusikan ke persamaan luas berikut. 

Untuk mengasah pemahaman Quipperian tentang materi integral, simak contoh-contoh soal berikut.

Contoh soal 1

Jika diketahui f '(x) = x + 2 dan nilai f(1) = , tentukan fungsi f(x)!
Pembahasan:
Untuk menentukan nilai f(x), Quipperian harus tahu bahwa fungsi f(x) merupakan bentuk integral dari f’(x).

Persamaan di atas masih memuat konstanta integrasi, c, sehingga Quipperian harus mencari nilai c tersebut dengan mensubstitusikan nilai fungsi yang diketahui.

Jadi, nilai fungsi yang diminta adalah sebagai berikut.

Contoh soal 2

Tentukan luas daerah yang diarsir pada gambar di bawah ini!

Pembahasan:
Tentukan batas-batasnya terlebih dahulu.

• Batas kanan:  x√y
• Batas kiri: sumbu y (x = 0)
• Batas atas: y = 9I
• Batas bawah: y = 0

Luas daerah yang diarsir adalah
Jadi, luas daerah yang diarsir adalah 18 satuan luas.

Contoh soal 3

Tentukan luas daerah yang dibatasi oleh y = x2 – 3x – 10 dengan y = x + 2!
Pembahasan:
Berdasarkan soal di atas, terlihat bahwa daerah dibatasi oleh 2 fungsi, yaitu fungsi kuadrat y = x2 – 3x – 10 dan fungsi linier y = x + 2, sehingga berlaku rumus cepat untuk luas.

Substitusikan nilai a, b, dan c yang sudah diperoleh ke dalam persamaan berikut.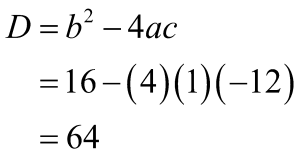

Luas daerahnya adalah sebagai berikut.

Nah, itulah pembahasan Quipper Blog kali ini tentang materi integral. Tanpa Quipperian sadari, integral dekat dengan kehidupan sehari-hari, terlebih jika sudah berinteraksi dengan dunia kerja. Salah satu contohnya integral biasa digunakan di bidang ekonomi untuk menganalisis tentang kinerja perusahaan meliputi hasil produksi, SDM, sampai bahan-bahannya.
Jika Quipperian ingin melihat lebih lanjut tentang penjelasan materi integral, silakan gabung dengan Quipper Video, yuk. Bersama Quipper Video, kalian bisa berjumpa dengan tutor-tutor kece yang pastinya selalu ada dimanapun dan kapanpun. So, tunggu apa lagi!

SUMBER :

• https://quipper.com
  
• https://id.wikipedia.org/wiki/Integral
• https://d14fikpiqfsi71.cloudfront.net/
• https://d14fikpiqfsi71.cloudfront.net/%5B/spoiler%5D

Penulis: Eka Viandari 

Catatan SDR:

 Modul Integral bisa didownload disini