Secara sederhana, relasi dapat diartikan sebagai hubungan. Hubungan
yang dimaksud di sini adalah hubungan antara daerah asal (domain) dan
daerah kawan (kodomain). Kedua jenis daerah akan dijelaskan kemudian.
Sedangkan fungsi adalah relasi yang memasangkan setiap anggota himpunan
daerah asal tepat satu ke himpunan daerah kawannya. Perbedaan antara
relasi dan fungsi terletak pada cara memasangkan anggota himpunan ke
daerah asalnya.
Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota
himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas
pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh
mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki
pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal
dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap
anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu
dipasangkan dengan daerah kawannya.
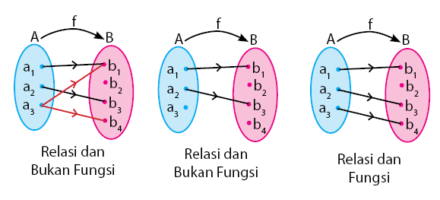
Kesimpulannya, setiap relasi belum tentu fungsi, namun setiap fungsi
pasti merupakan relasi. Penjelasan mengenai relasi dan fungsi dapat
dilihat pada gambar di bawah.
Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah.
Baca Juga: Sifat-sifat dan Contoh Soal Komposisi Fungsi
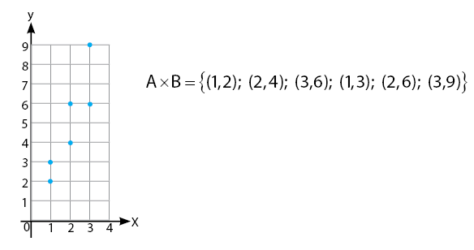
Cara menyatakan hasil relasi perkalian antara himpunan A dan B dapat dilihat pada contoh permasalahan di bawah.
![Rendered by QuickLaTeX.com \[ A \; = \; \left \{ 1, \; 2, \; 3, \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d1fee107072593e46e96febee4dec418_l3.svg)
![Rendered by QuickLaTeX.com \[ B \; = \; \left \{ 2, 3 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-daeb4c427f2ec88d2832af6982ed15e9_l3.svg)
Pembahasan selanjutnya adalah mengenai fungsi, simak dengan baik sammpai akhir ya!
Simbol fungsi yang memetakan himpunan A ke B adalah
![Rendered by QuickLaTeX.com \[ f: \; A \rightarrow B\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6fcd2503c617afc66fb662d8ac5083a0_l3.svg) Contoh pemasalahan pada fungsi:
Contoh pemasalahan pada fungsi:
Diketahui himpunan A dan B diberikan seperti di bawah.
![Rendered by QuickLaTeX.com \[ A = \left \{ 0, 1, 2, 3, 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-643bf49e5f45e692e5a4ffca0538aaeb_l3.svg)
![Rendered by QuickLaTeX.com \[ B = \left \{ 0, 1, 2, ..., 10 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-440212b7cc191c741c4a0aba87d632a9_l3.svg) Didefinisikan fungsi
Didefinisikan fungsi  dengan f(x) = x + 5.
dengan f(x) = x + 5.
Tentukan hasil pemetaan dari oleh fungsi
oleh fungsi  ,
,  ,
,  , dan
, dan  !
!
Pembahasan:
Peta dari oleh fungsi f yaitu y = f(x):
oleh fungsi f yaitu y = f(x):
![Rendered by QuickLaTeX.com \[ f(0) = 0 + 5 = 5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c4ebb9c99c38503f006f99eb66e3b0db_l3.svg)
![Rendered by QuickLaTeX.com \[ f(1) = 1 + 5 = 6 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d2118a577e3819445aa95e455f670d67_l3.svg)
![Rendered by QuickLaTeX.com \[ f(2) = 2 + 5 = 7 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-03b90256b4833280c8bba9ebac02eafe_l3.svg)
![Rendered by QuickLaTeX.com \[ f(3) = 3 + 5 = 8 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-9c26831a27c317d4dcb853763c6221b9_l3.svg)
![Rendered by QuickLaTeX.com \[ f(4) = 4 + 5 = 9 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-eee345654dad9700db41710aaf317543_l3.svg)
 = Daerah Asal
= Daerah Asal
![Rendered by QuickLaTeX.com \[ D_{f} = A = \left \{ 0, 1, 2, 3, 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0e91b7c13ff17e363486f70d260275d6_l3.svg)
 = Daerah Kawan
= Daerah Kawan
![Rendered by QuickLaTeX.com \[ K_{f} = B = \left \{ 0, 1, 2, ..., 10 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ed9c47be5a6fc3133226b166bf608a00_l3.svg)
Daerah Hasil =
![Rendered by QuickLaTeX.com \[ D_{f} = A = \left \{5, 6, 7, 8, 9 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-31e10c571e8cd9ebd151c45afe542a75_l3.svg) Baca Juga: Contoh Persaamaan Matematika yang Merupakan Fungsi
Baca Juga: Contoh Persaamaan Matematika yang Merupakan Fungsi
Pernahkah kalian melihat atau mendengar menara Pisa di Italia? Menara Pisa adalah sebuah menara lonceng yang memiliki kemiringan sekitar 50namun tetap berdiri hingga saat ini. Menara Pisa didirikan pada Abad ke-12.
Tahukah kamu, bagaimana menentukan sudut kemiringan dari Menara Pisa ini? Untuk menentukan kemiringan kita bisa menggunakan konsep dari persamaan garis lurus dengan membuat koordinat Kartesiusnya. Aplikasi persamaan garis lurus tidak hanya untuk menentukan kemiringan suatu bangunan namun juga dapat menentukan waktu dan jarak dari kecepatan yang diperoleh, peramalan harga atau jumlah penduduk di tahun tertentu. Menarik, bukan?
So, pada kesempatan kali ini, Quipper Blog akan membahas tentang garis lurus dan persamaannya, penentuan nilai gradien, serta contoh soal dan pembahasan aplikasi persamaan garis lurus dari bank soal Quipper Video yang selalu update. Yuk, simak!

Di mana
y = persamaan garis lurus,
m = gradien/ kemiringan,
c = konstanta,
a dan b merupakan suatu variabel.

Dari gambar di atas dapat dijelaskan bahwa f(x) = 2x + 1 disebut garis lurus, di mana nilai gradien dari garis tersebut adalah 2 dan konstantanya adalah 1. Garis lurus tersebut berjenis y = mx + c.

Persamaan diatas dapat digunakan apabila garis dihubungkan dengan dua titik X (x2, x1) dan Y (y2, y1). Sedangkan untuk menentukan gradien dari persamaan garis lurus secara implisit (ax + by + c = 0) adalah sebagai berikut:

Apabila suatu soal diketahui nilai gradiennya dan titik koordinatnya A (x1,y1). Maka persamaan garis lurus dapat ditentukan menggunakan persamaan:

Namun apabila di soal terdiri dari dua titik A (x1,y1) dan B (x2,y2). Persamaan garis lurus dapat ditentukan menggunakan persamaan:
Untuk menjawab soal di atas kita dapat menggunakan rumus persamaan garis di antara dua titik yaitu:

2. Diketahui sebuah garis lurus yaitu 8x + 4y + 9 = 0. Tentukan nilai gradien dari garis lurus tersebut.
Untuk menjawab soal di atas, kita mengetahui bahwa garis tersebut adalah garis lurus implisit. Sehingga nilai gradiennya dapat dicari dengan:

3. Tentukan persamaan garis yang melalui titik (2, 3) dan sejajar dengan garis y = 2x – 5.
Diketahui nilai gradiennya adalah ( m=2). Maka nilai persamaan garis lurusnya adalah:

Jadi nilai persamaan garis lurusnya adalah y = 2x -1

Nilai gradien dapat ditentukan dari suatu hubungan dari garis-garis yang ada. Contohnya garis-garis yang sejajar dan garis-garis yang saling tegak lurus. Bunyi hukum gradien suatu garis adalah sebagai berikut “Garis-garis yang sejajar mempunyai gradien yang sama dan hasil kali gradien garis-garis yang saling tegak lurus adalah 1”.

Dari gambar di atas, terlihat ada 4 garis yaitu (garis a, garis b, garis c, dan garis d). Untuk menentukan nilai gradien/kemiringan dari masing-masing tersebut, maka nilai gradiennya dapat diperoleh menggunakan persamaan:

Sehingga gradient garis a adalah

Gradien garis b adalah

Gradien garis c adalah

Gradien garis d adalah

Nilai Gradien dari ke-4 garis tersebut adalah sama yaitu 5/4. Hal ini dikarenakan ke-4 garis tersebut adalah saling sejajar. Sedangkan di bawah ini adalah cara menentukan nilai gradien garis yang saling tegak lurus.

Gradien garis k adalah
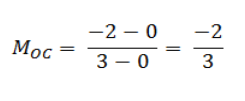
Gradien garis h adalah

Perhatikan bahwa perkalian gradien garis h dan garis k diperoleh:

Penerapan konsep dari persamaan garis lurus tidak hanya dapat menentukan nilai kemiringan suatu bangunan namun juga dapat digunakan untuk menentukan permasalahan penting lainnya dalam kehidupan sehari-hari yaitu jarak dan waktu dari suatu kecepatan, peramalan harga suatu barang dalam kurun waktu tertentu, serta peramalan jumlah penduduk dari suatu wilayah. Berikut contoh soal dan pembahasannya.

Permasalahan di atas dapat diselesaikan menggunakan rumusan persamaan garis dengan membuat satu titik tetap yang kita sebut titik asal. Pada saat mula-mula posisi orang berada di titik s = 0 (titik asal) dan setiap detik bergerak ke kanan, pesepeda tersebut bergerak sejauh 3 km. Posisi orang tersebut dapat dilihat pada tabel di bawah ini:

Dengan t menyatakan waktu dan s menyatakan posisi/jarak, sehingga hubungan antara s dan t dapat disajikan dalam bentuk persamaan S = 15t
Untuk menggambar garis tersebut dapat dilakukan cara dengan membuat koordinat kartesisus dengan menghubungkan pasangan titik pada tabel di atas yaitu (0,0), (1,15), (2,30), (3,45), sehingga grafik persamaan s = 15 t dapat disajikan pada gambar di bawah ini.

Perhatikan bahwa sumbu horizontal menyatakan waktu (t) dan sumbu vertikal menyatakan jarak yang ditempuh (s). Bilangan 15 pada persamaan gerak s = 15 t disebut kecepatan benda atau gradien garis tersebut. Berdasarkan hubungan ini, untuk mencari posisi benda pada waktu atau mencari waktu pada posisi tertentu, cukup dengan menggantikan nilai t pada persamaan tersebut. Sehingga untuk mencari t pada s = 90 km, persamaannya:

Diasumsikan variabel x sebagai kurun waktu dalam tahun dan y sebagai nilai harga dalam rupiah. Dari soal diketahui bahwa y = Rp50.000.000 jika x = 0. Misalkan gradiennya adalah m maka m = 200.000 (karena tiap tahun bertambah Rp200.000)
Sehingga diperoleh persamaan harga sebagai berikut:

Untuk x = 5 tahun, maka harga yang diperoleh adalah

Jadi harga tanah setelah 5 tahun adalah Rp51.000.000.
Untuk menyelesaikan soal di atas kita misalkan x sebagai waktu dan y menyatakan jumlah penduduk. Karena pertambahan penduduk tiap tahunnya tetap, berarti grafik jumlah penduduk terhadap waktu merupakan garis lurus dengan persamaan sebagai berikut:

Untuk x = 2015, maka nilai y = 500.000 (2015-2005) + 600.000 = 1.100.000
Jadi pertumbuhan penduduk pada tahun 2015 adalah 1.100.000 orang.
Bagaimana Quipperian mulai tertarik kan belajar konsep-konsep Matematika? Ternyata apabila kita memahami konsep dasar dari Matematika maka Quipperian dapat menjelaskan masalah-masalah nyata menggunakan konsep matematika juga. Apabila Quipperian ingin memahami masalah-masalah nyata menggunakan konsep Matematika, mari bergabung bersama Quipper Blog, karena masih banyak penjelasan yang menarik dan mudah dipahami untuk membantu Quipperian menyelesaikan masalah-masalah nyata menggunakan konsep Matematika.
Sumber:

Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah.
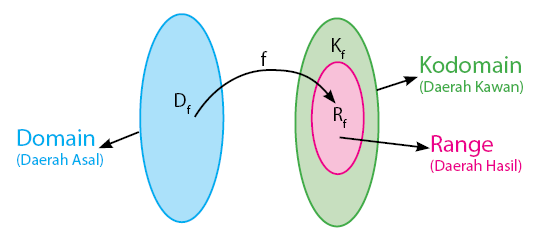
Daerah Asal, Kawan, dan Hasil
Dalam pembahasan relasi dan fungsi, himpunan yang terlibat digolongkan ke dalam tiga jenis daerah. Ketiga daerah tersebut adalah daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Secara umum, himpunan ketiga daerah tersebut dapat dilihat pada gambar di bawah.
Baca Juga: Sifat-sifat dan Contoh Soal Komposisi Fungsi
Relasi
Seperti yang telah dijelaskan secara singkat di atas, relasi dapat diartikan sebagai hubungan. Misalkan sebuah relasi menyatakan hubungan perkalian. Hasil relasi tersebut dapat dinyatakan dalam himpunan pasangan terurut x dan y dan dapat juga digambar pada bidang kartesius.Cara menyatakan hasil relasi perkalian antara himpunan A dan B dapat dilihat pada contoh permasalahan di bawah.

Pembahasan selanjutnya adalah mengenai fungsi, simak dengan baik sammpai akhir ya!
Fungsi atau Pemetaan
Fungsi atau yang sering disebut juga dengan pemetaan masih termasuk dalam relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya.Simbol fungsi yang memetakan himpunan A ke B adalah
Diketahui himpunan A dan B diberikan seperti di bawah.
Tentukan hasil pemetaan dari
Pembahasan:
Peta dari
Daerah Hasil =
Sifat-sifat Fungsi
Fungsi dikelompokkan menjadi 3 (tiga) jenis yaitu fungsi Injektif, Surjektif, dan Bijektif. Pengelompokkan tersebut didasarkan pada sifatnya. Perbedaan ketiga jenis tersebut dapat disimak pada penjelasan di bawah.- Fungsi Injektif/Fungsi Into (Fungsi Satu-satu)
Fungsi pertama yang akan dibahas adalah fungsi injektif atau sering disebut dengan fungsi into atau fungsi satu-satu. Fungsi
dikatakan fungsi injektif jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain.
Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, namun semua anggota kodomain yang terpsangkan hanya ada satu, tidak boleh ada yang lebih dari satu.
Perhatikan gambar di bawah untuk melihat lebih detail mengenai perbedaannya.

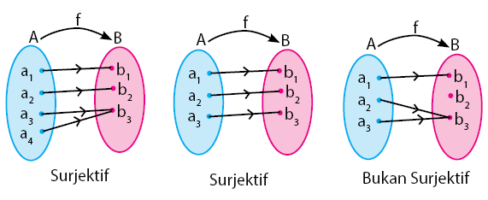
- Fungsi Surjektif (Fungsi Onto)
Fungsi Surjekti atau onto memiliki ciri yaitu anggota kodomainnya
boleh memiliki pasangan lebih dari satu, namun tidak boleh ada anggota
kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi
apabila jumlah anggota kodomain sama atau lebih banyak dari anggota
domain.
Perhatikan gambar di bawah untuk menambah pemahan sobat idschool tentang sifat fungsi surjektif.
- Fungsi Bijektif (Korespondensi Satu-satu)
Fungsi Bijektif merupakan gabungan dari fungsi injektif dan
surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain
terpasangkan tepat satu. Kebalikan fungsi dari fungsi injektif dan
surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari
fungsi bijektif juga merupakan fungsi/pemetaan. Perhatikan gambar di
bawah.

Terlihat bahwa kebalikan dari fungsi f juga merupakan fungsi atau pemetaan, bukan?
Sumber: https://idschool.net
Pernahkah kalian melihat atau mendengar menara Pisa di Italia? Menara Pisa adalah sebuah menara lonceng yang memiliki kemiringan sekitar 50namun tetap berdiri hingga saat ini. Menara Pisa didirikan pada Abad ke-12.
Tahukah kamu, bagaimana menentukan sudut kemiringan dari Menara Pisa ini? Untuk menentukan kemiringan kita bisa menggunakan konsep dari persamaan garis lurus dengan membuat koordinat Kartesiusnya. Aplikasi persamaan garis lurus tidak hanya untuk menentukan kemiringan suatu bangunan namun juga dapat menentukan waktu dan jarak dari kecepatan yang diperoleh, peramalan harga atau jumlah penduduk di tahun tertentu. Menarik, bukan?
So, pada kesempatan kali ini, Quipper Blog akan membahas tentang garis lurus dan persamaannya, penentuan nilai gradien, serta contoh soal dan pembahasan aplikasi persamaan garis lurus dari bank soal Quipper Video yang selalu update. Yuk, simak!
Pengertian Garis Lurus & Gradien

Garis Lurus
Garis lurus adalah kumpulan titik-titik yang tak berhingga dan saling berdampingan. Garis lurus dapat dinyatakan ke dalam suatu persamaan eksplisit dan implisit. Persamaan garis lurus secara eksplisit contohnya yaitu y = mx dan y = mx + c sedangkan persamaan garis lurus secara implisit adalah ax + by + c = 0.Di mana
y = persamaan garis lurus,
m = gradien/ kemiringan,
c = konstanta,
a dan b merupakan suatu variabel.

Dari gambar di atas dapat dijelaskan bahwa f(x) = 2x + 1 disebut garis lurus, di mana nilai gradien dari garis tersebut adalah 2 dan konstantanya adalah 1. Garis lurus tersebut berjenis y = mx + c.
Gradien
Gradien adalah nilai kemiringan suatu garis. Gradien dapat bernilai positif atau negatif. Sesuai perjanjian gradien bernilai positif apabila arah garis ke kanan dan ke atas sedangkan gradien bernilai negatif apabila arah garis ke kiri dan ke bawah. Secara umum, nilai suatu gradien garis dapat dinyatakan dalam suatu rumusan matematis yaitu:
Persamaan diatas dapat digunakan apabila garis dihubungkan dengan dua titik X (x2, x1) dan Y (y2, y1). Sedangkan untuk menentukan gradien dari persamaan garis lurus secara implisit (ax + by + c = 0) adalah sebagai berikut:

Apabila suatu soal diketahui nilai gradiennya dan titik koordinatnya A (x1,y1). Maka persamaan garis lurus dapat ditentukan menggunakan persamaan:

Namun apabila di soal terdiri dari dua titik A (x1,y1) dan B (x2,y2). Persamaan garis lurus dapat ditentukan menggunakan persamaan:
Contoh soal
1. Diketahui garis lurus melalui titik A (-4, 5) dan B (2, 3). Tentukan nilai dari gradien tersebut.Untuk menjawab soal di atas kita dapat menggunakan rumus persamaan garis di antara dua titik yaitu:

2. Diketahui sebuah garis lurus yaitu 8x + 4y + 9 = 0. Tentukan nilai gradien dari garis lurus tersebut.
Untuk menjawab soal di atas, kita mengetahui bahwa garis tersebut adalah garis lurus implisit. Sehingga nilai gradiennya dapat dicari dengan:

3. Tentukan persamaan garis yang melalui titik (2, 3) dan sejajar dengan garis y = 2x – 5.
Diketahui nilai gradiennya adalah ( m=2). Maka nilai persamaan garis lurusnya adalah:

Jadi nilai persamaan garis lurusnya adalah y = 2x -1
Menentukan Nilai Gradien

Nilai gradien dapat ditentukan dari suatu hubungan dari garis-garis yang ada. Contohnya garis-garis yang sejajar dan garis-garis yang saling tegak lurus. Bunyi hukum gradien suatu garis adalah sebagai berikut “Garis-garis yang sejajar mempunyai gradien yang sama dan hasil kali gradien garis-garis yang saling tegak lurus adalah 1”.

Dari gambar di atas, terlihat ada 4 garis yaitu (garis a, garis b, garis c, dan garis d). Untuk menentukan nilai gradien/kemiringan dari masing-masing tersebut, maka nilai gradiennya dapat diperoleh menggunakan persamaan:

Sehingga gradient garis a adalah

Gradien garis b adalah

Gradien garis c adalah

Gradien garis d adalah

Nilai Gradien dari ke-4 garis tersebut adalah sama yaitu 5/4. Hal ini dikarenakan ke-4 garis tersebut adalah saling sejajar. Sedangkan di bawah ini adalah cara menentukan nilai gradien garis yang saling tegak lurus.

Gradien garis k adalah
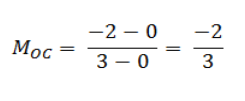
Gradien garis h adalah

Perhatikan bahwa perkalian gradien garis h dan garis k diperoleh:

Penerapan konsep dari persamaan garis lurus tidak hanya dapat menentukan nilai kemiringan suatu bangunan namun juga dapat digunakan untuk menentukan permasalahan penting lainnya dalam kehidupan sehari-hari yaitu jarak dan waktu dari suatu kecepatan, peramalan harga suatu barang dalam kurun waktu tertentu, serta peramalan jumlah penduduk dari suatu wilayah. Berikut contoh soal dan pembahasannya.
Latihan Soal, Yuk!

Nomor 1
Seseorang bersepeda dengan kecepatan tetap 15 km/jam. Setelah 3 jam, orang tersebut menempuh jarak 45 km. Berapa lama waktu yang diperlukan orang tersebut untuk menempuh jarak 90 km?Permasalahan di atas dapat diselesaikan menggunakan rumusan persamaan garis dengan membuat satu titik tetap yang kita sebut titik asal. Pada saat mula-mula posisi orang berada di titik s = 0 (titik asal) dan setiap detik bergerak ke kanan, pesepeda tersebut bergerak sejauh 3 km. Posisi orang tersebut dapat dilihat pada tabel di bawah ini:

Dengan t menyatakan waktu dan s menyatakan posisi/jarak, sehingga hubungan antara s dan t dapat disajikan dalam bentuk persamaan S = 15t
Untuk menggambar garis tersebut dapat dilakukan cara dengan membuat koordinat kartesisus dengan menghubungkan pasangan titik pada tabel di atas yaitu (0,0), (1,15), (2,30), (3,45), sehingga grafik persamaan s = 15 t dapat disajikan pada gambar di bawah ini.

Perhatikan bahwa sumbu horizontal menyatakan waktu (t) dan sumbu vertikal menyatakan jarak yang ditempuh (s). Bilangan 15 pada persamaan gerak s = 15 t disebut kecepatan benda atau gradien garis tersebut. Berdasarkan hubungan ini, untuk mencari posisi benda pada waktu atau mencari waktu pada posisi tertentu, cukup dengan menggantikan nilai t pada persamaan tersebut. Sehingga untuk mencari t pada s = 90 km, persamaannya:

Nomor 2
Sebidang tanah dengan harga perolehan Rp50.000.000 diperkirakan mengalami tingkat kenaikan konstan Rp200.000 per tahun dalam kurun waktu 5 tahun. Tentukan persamaan garis harga tanah tersebut dan harga tanah setelah 5 tahun!Diasumsikan variabel x sebagai kurun waktu dalam tahun dan y sebagai nilai harga dalam rupiah. Dari soal diketahui bahwa y = Rp50.000.000 jika x = 0. Misalkan gradiennya adalah m maka m = 200.000 (karena tiap tahun bertambah Rp200.000)
Sehingga diperoleh persamaan harga sebagai berikut:

Untuk x = 5 tahun, maka harga yang diperoleh adalah

Jadi harga tanah setelah 5 tahun adalah Rp51.000.000.
Nomor 3
Di salah satu kota X di Pulau Jawa, pertambahan penduduk tiap tahunnya selalu tetap. Pada tahun 2005 dan tahun 2011, jumlah penduduk di kota itu berturut-turut 600.000 orang dan 900.000 orang. Berapa jumlah penduduk di kota itu pada tahun 2015?Untuk menyelesaikan soal di atas kita misalkan x sebagai waktu dan y menyatakan jumlah penduduk. Karena pertambahan penduduk tiap tahunnya tetap, berarti grafik jumlah penduduk terhadap waktu merupakan garis lurus dengan persamaan sebagai berikut:

Untuk x = 2015, maka nilai y = 500.000 (2015-2005) + 600.000 = 1.100.000
Jadi pertumbuhan penduduk pada tahun 2015 adalah 1.100.000 orang.
Bagaimana Quipperian mulai tertarik kan belajar konsep-konsep Matematika? Ternyata apabila kita memahami konsep dasar dari Matematika maka Quipperian dapat menjelaskan masalah-masalah nyata menggunakan konsep matematika juga. Apabila Quipperian ingin memahami masalah-masalah nyata menggunakan konsep Matematika, mari bergabung bersama Quipper Blog, karena masih banyak penjelasan yang menarik dan mudah dipahami untuk membantu Quipperian menyelesaikan masalah-masalah nyata menggunakan konsep Matematika.
Sumber:
- Dhoruri, Atmini. 2011. Pembelajaran Persamaan Garis Lurus di SMP.Jakarta: Kemdikbud
- Insani, Nur. 2007. Kalkulus Differensial.Yogyakarta: Universitas Negeri Yogyakarta
- Tampomas, Husein. 2007. Seribu Pena Matematika Jilid 2 untuk SMA/MA kelas XI. Jakarta: Erlangga
- https://sport.tempo.co/read/1162215/kejuaraan-balap-sepeda-asia-di-jakarta-indonesia-targetkan-juara
- https://sejarahnasionaldandunia.blogspot.com/2017/05/peta-pulau-jawa-lengkap-dengan.html
- https://www.liputan6.com/global/read/2869059/27-2-1964-terancam-ambruk-menara-miring-pisa-dinyatakan-kritis

Komentar
Posting Komentar
Tiada gading yang tak retak, saran dan masukan Anda akan sangat membantu kami. Budayakan Membaca Sampai Akhir, Jika ada yang masih kurang jelas, Anda dapat menuliskannya pada kolom komentar di bawah ini atau melalui Contact Us di bagian blog ini.
1. Centang kotak Notify me untuk berlangganan.
2. Setiap Komentar yang masuk akan kami moderasi, sebelum tampil dipublish.
3. Patuhi pedoman berkomentar dengan sopan santun dan menghargai pendapat orang lain.
Semoga kedepannya kita dapat bekerja sama dengan baik!
Salam Sukses dan Bahagia.