Materi Bilangan Real

Bilangan Real

Dalam matematika menyatakan bilangan yang bisa dituliskan dalam bentuk desimal, seperti 2,4871773339… atau 3,25678. Bilangan real meliputi bilangan rasional, seperti 42 dan −23/129, dan bilangan irasional, seperti π dan . Bilangan riil juga dapat dilambangkan sebagai salah satu titik dalam garis bilangan.

Definisi popular dari bilangan real meliputi klas ekuivalen dari deret Cauchy rasional, irisan Dedekind dan deret Archimides.

Bilangan riil ini berbeda dengan bilangan kompleks yang termasuk di dalamnya adalah bilangan imajiner.

Sifat-sifat operasi Bilangan Real

Sifat-sifat yang berlaku pada bilangan real dengan operasi “penjumlahan” dan “perkalian”.

Untuk setiap   , beralaku sifat-sifat berikut;

Penjumlahan:

1. Sifat tertutup pada penjumlahan;

2. Sifat komutatif pada penjumlahan

3. Sifat asosiatif pada penjumlahan

4. Sifat distributif perkalian terhadap penjumlahan

5. Sifat identitas pada penjumlahan (0 adalah elemen identitas atau elemen netral)

6. Sifat invers pada penjumlahan

Perkalian:

1. Sifat tertutup pada perkalian

2. Sifat komutatif pada perkalian

3. Sifat asosiatif pada perkalian

4. Sifat distributif perkalian terhadap penjumlahan

5. Sifat identitas pada perkalian (1 adalah elemen identitas perkalian)

6. Sifat invers pada perkalian tidak berlaku, sebab 0 tidak mempunyai invers.

(untuk )

(tidak ada/tidak didefinisikan).

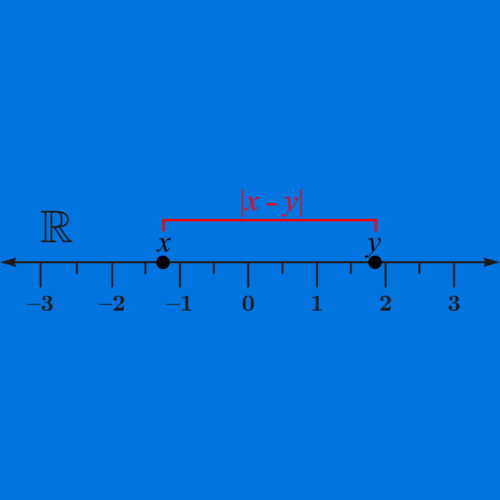
Menunjukkan perbedaan mutlak antara dua bilangan real sebagai jarak antara titik-titik yang sesuai pada garis real. Sumber foto: Wikipedia

Sifat-sifat bilangan real

Aksioma medan

Bilangan riil, beserta operasi penjumlahan dan perkalian, memenuhi aksioma (yang berarti dianggap berharga atau sesuai atau dianggap terbukti dengan sendirinya) berikut. Misalkan x,y dan z merupakan anggota himpunan bilangan riil R, dan operasi x+y merupakan penjumlahan, serta xymerupakan perkalian. Maka:

• Aksioma 1 (hukum komutatif): x+y = y+x, dan xy = yx
• Aksioma 2 (hukum asosiatif): x+(y+z) = (x+y)+z dan x(yz) = (xy)z
• Aksioma 3 (hukum distributif): x(y+z) = (xy + xz)
• Aksioma 4: Eksistensi unsur identitas. Terdapat dua bilangan riil berbeda, yang dilambangkan sebagai 0 dan 1, sehingga untuk setiap bilangan riil x kita mendapatkan 0+x=x dan 1.x=x.
• Aksioma 5: Eksistensi negatif, atau invers terhadap penjumlahan. Untuk setiap bilangan riil x, terdapat bilangan riil y sehingga x+y=0. Kita dapat juga melambangkan y sebagai -x.
• Aksioma 6: Eksistensi resiprokal, atau invers terhadap perkalian. Untuk setiap bilangan riil x tidak sama dengan 0, terdapat bilangan riil y sehingga xy=1. Kita dapat melambangkan y sebagai 1/x.

Himpunan yang memenuhi sifat-sifat ini disebut sebagai medan, dan karena itu aksioma di atas dinamakan sebagai aksioma medan.

Aksioma urutan

Kita akan mengasumsikan terdapat himpunan R+, yang disebut sebagai bilangan positif yang merupakan himpunan bagian dari R. Misalkan juga x dan y adalah anggota R+. Himpunan bagian ini memenuhi aksioma urutan berikut:

• Aksioma 7: x+y dan xy merupakan anggota R+
• Aksioma 8: Untuk setiap x yang tidak sama dengan 0, x anggota R+ atau -x anggota R+, tetapi tidak mungkin keduanya sekaligus
• Aksioma 9: 0 bukan anggota R+.

 Garis bilangan takterhingga yang menggambarkan bilangan riil

Aksioma kelengkapan

• Aksioma 10: Setiap himpunan bilangan riil S yang memiliki batas atas memiliki supremum, yakni ada suatu bilangan riil B sehingga B=sup(S).

Operasi penjumlahan, pengurangan, perkalian, dan pembagian

1. Operasi penjumlahan

Contoh:

1. 

2. 

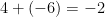
3. 

4. 

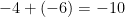
2. Operasi pengurangan

Contoh:

1. 

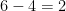
2. 

3. -6 – 4 = -6 + (-4) = -10 $

3. Operasi perkalian

Contoh:

1. 

2. 

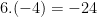
3. 

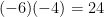
4. Operasi pembagian

Contoh:

Pengubahan pecahan ke desimal, desimal ke persen dan sebaliknya

1. Mengubah Pecahan Biasa ke Desimal

Contoh:

2. Mengubah Pecahan Desimal ke Persen

Contoh:

c) Mengubah persen ke pecahan dan sebaliknya

Contoh:

Nyatakan ke dalam pecahan atau ke dalam persen!

Contoh soal dan jawaban bilangan real

1. Sebuah koperasi sekolah membeli lima lusin buku seharga Rp. 150.000,00. Jika harga jual sebuah buku Rp. 2.800,00, maka persentase keuntungan yang diperoleh koperasi tersebut adalah…

a) 4%
b) 6%
c.  10%
d.  12%
e.  14%

Jawab : d. 12%

Cara Untung = harga jual – harga beli

        = Rp.168.000,00 – Rp.150.000,00

        = Rp.  18.000,00

% Untung = Untung

        H.B

  = Rp. 18.000,00 x 100% = 12%

     Rp. 150.000,00

2. Sebuah toko baju ada memberikan diskon sebesar 25% untuk semua produk. Jika kita berbelanja senilai Rp. 800.000,00, berapa kita harus membayar?

Jawab:

Diskon = 25 % x Rp. 800.000,00

Jadi, kita harus membayar sebesar:

Rp. 800.000,00 – Rp. 200.000,00 = Rp. 600.000,00

3. Sebuah TV dibeli dengan harga Rp. 2.000.000,00, dan di jual dengan harga Rp. 2.400.000,00. Hitunglah persentase keuntungan dari harga pembelian dan dari harga penjualan!

Jawab:

Laba = Rp. 2.400.000,00 – Rp. 2.000.000,00 = Rp. 400.000,00

Persentase keuntungan (laba) dari harga beli:

Persentase keuntungan (laba) dari harga penjualan:

4. Beras dibeli dengan harga Rp.168.000,00 per-50kg, kemudian dijual harga Rp.2.100,00 tiap ½ kg. Persentase keuntungan dari harga pembelian adalah…

a) 10%
b) 15%
c) 23%
d. 30%
e. 35%

Jawaban: c 25%

Cara menghitung Untung = harga jual – harga beli

        = Rp.210.000,00 – Rp.168.000,00

        = Rp.  42.000,00

% Untung =    U

       H.B

  = Rp. 42.000,00 x 100% = 25%

     Rp. 168.000,00

Sumber: https://www.pinterpandai.com

Catatan SDR:

Modul pertemuan pertama silahkan coba klik tautan berikut

Pembahasan Latihan 1-4 ada di YouTube +-3 menit: